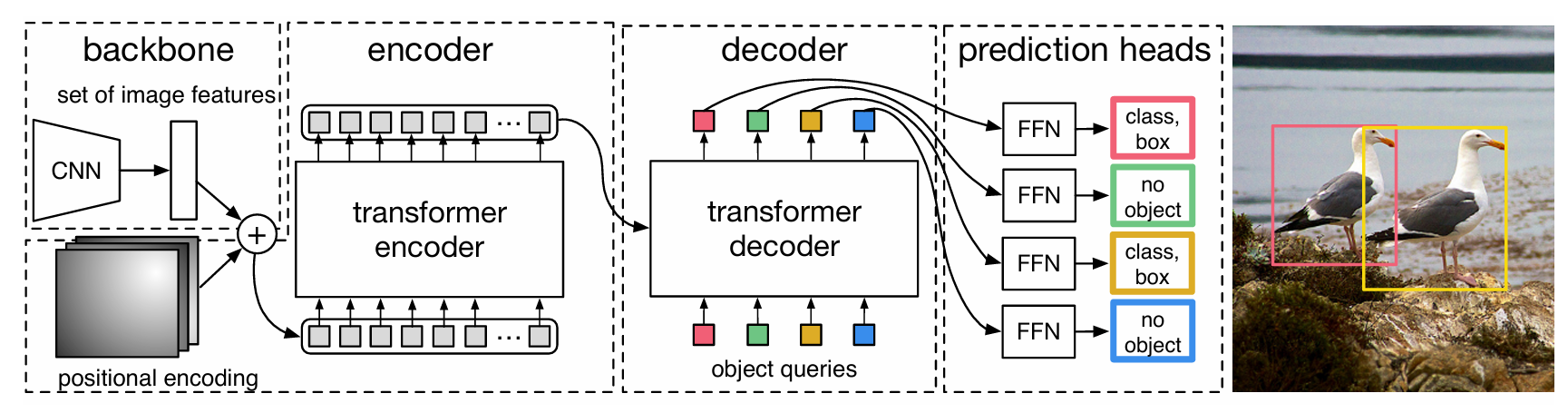
背景

传统的目标检测方法通常采用非直接的方法来实现，通常需要设计一种方法在一大堆建议集中通过代理回归和分类的方式来找到目标框和目标类别。但是这种方法的性能极大的受后处理算法的影响（因为要去掉大量近邻的重复预测结果，即一个目标被多个识别框选中）。为了简化这一流程，本论文设计了一种直接预测集合的方法来直接跳过代理任务（意思就是DETR输出的结果就是我们想要的预测框和类别，而不再需要通过NMS等后处理手段对输出的结果进行处理）。

模型整体结构

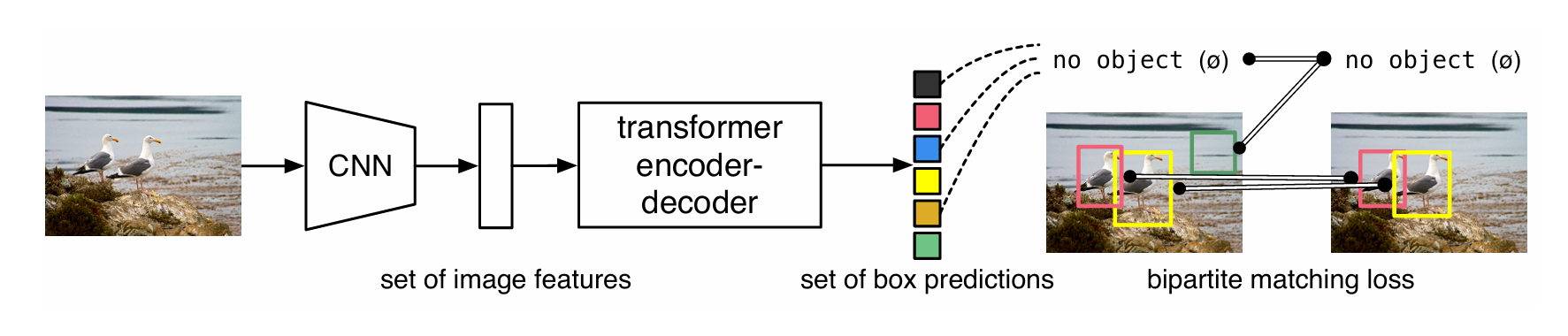
DETR采用了encoder-decoder的结构。对于输入的原始图像，首先经过一个CNN将其转换为Patch，然后经过Transformer Encoder-Decoder并行得到一系列固定数量的预测框（这些预测框是通过一个FFN对Transformer Encoder-Decoder重构的特征映射为类别和bbox的）。在训练时，会使用二分匹配对预测框和GT进行匹配，确保了预测框和GT之间的一一对应关系，同时，用匹配后的结果计算loss也可以保证即使输出的预测框顺序不一样也不会对loss的值产生影响（也就是论文中写的invariant to a permutation of predicted objects）。此外，DETR没有使用NLP中常用的Auto-Regressive Transformer Decoder，而是使用了并行的Decoder来进行解码。

此外，作者在论文中提到，DETR虽然在常规目标检测任务中表现出众，但在小目标检测中表现欠佳，作者提到可以考虑使用FPN特征金字塔来进行优化。另外作者还提到，这个模型需要很长的训练周期，并且使用auxiliary decoding losses会对模型的训练有用。对了，作者还提到：DETR不仅可以解决分类问题，如果对DETR的输出Head进行适当的修改也是可以做分割等任务的。

技术细节

概述

要实现直接进行集合式的预测，需要考虑以下几个方面：

• Loss函数需要实现对预测结果和GT的一一映射
• 模型结构需要并行地输出一系列检测目标并且对这些检测目标之间的关系进行建模

损失函数设计

DETR的推理输出是固定的N个预测框（N通常被设置为一个远大于正常图片中拥有的目标数量的整数），记为\hat{y}=\{\hat{y}_i\}^{N}_{i=1}，假设目标的GT为y（注：对y用no object进行padding，使之也有N个元素）。
为了保证\hat{y}的输出顺序不会对loss值产生影响，我们需要通过一种方法将\hat{y}与y进行一一对应匹配。优化目标就是寻找一种匹配规则，使得\hat{y}与y之间的匹配loss最小。论文作者将\hat{y}_i与y_i之间的匹配loss定义为：

\mathcal{L}_{match}(y_i,\hat{y}_i)=-\mathbb{1}_{\{c_i \neq \varnothing \} } \hat{\mathcal{p}}_{\sigma(i)}(c_i) + \mathbb{1}_{\{c_i \neq \varnothing \} } \mathcal{L}_{box}(b_i,\hat{b}_{\sigma(i)})

其中，c_i表示第i个GT的类别；b_i是一个长度为4的向量，每个元素的取值范围是[0,1]，分别表示相对于原图的预测框中心坐标和预测框的长宽；-\mathbb{1}_{\{c_i \neq \varnothing \} }为指示函数，表示当GT的类别不是no object时取1，否则取0；\sigma(i)表示第i个GT映射到的预测框的下标；\hat{\mathcal{p}}_{\sigma(i)}(c_i)表示；\hat{\mathcal{p}}_{\sigma(i)}(c_i)表示第\sigma(i)个预测框（即第i个GT所匹配的预测框）被分类为c_i的概率；\hat{b}_{\sigma(i)}表示第i个GT所匹配的预测框的中心坐标与长宽（相对）。

通过最小化\mathcal{L}_{match}，就可以得到GT与预测框之间的一一映射关系。在得到了这个映射关系后就可以计算\hat{y}_i与y_i之间的loss\mathcal{L}_{Hungarian}(y,\hat{y})。

\mathcal{L}_{Hungarian}(y,\hat{y})=\sum_{i=1}^{N} {-log \hat{\mathcal{p}}_{\sigma(i)}(c_i) + \mathbb{1}_{\{c_i \neq \varnothing \} } \mathcal{L}_{box}(b_i,\hat{b}_{\sigma(i)})}

在实际的训练过程中，为了避免目标与背景样本数量的不平衡(通常100个样本中，大部分都是背景)，当GT的类别为no object时，需要乘上一个因子\frac{1}{10}。特别地，当\hat{c}_{\sigma(i)}与c_i中间有一方是目标，一方是背景时，这一项loss应该是一个常数（与预测情况无关）。

在上面这个公式中，Bbox的loss\mathcal{L}_{box}不可以直接使用L1 loss，因为对于不同大小的Bbox，L1 loss不能很好的反映这种尺度上的不同。所以，本论文的\mathcal{L}_{box}通过对L1 loss和广义 IoU loss加权得到（IoU计算的是GT与预测框之间的重叠程度，可以消除尺度大小的影响）。

另外，论文里还提到了一个点：之所以在寻找匹配时没有对概率进行对数化处理，是因为这样可以让前后两个部分差不多大。

DETR详细结构

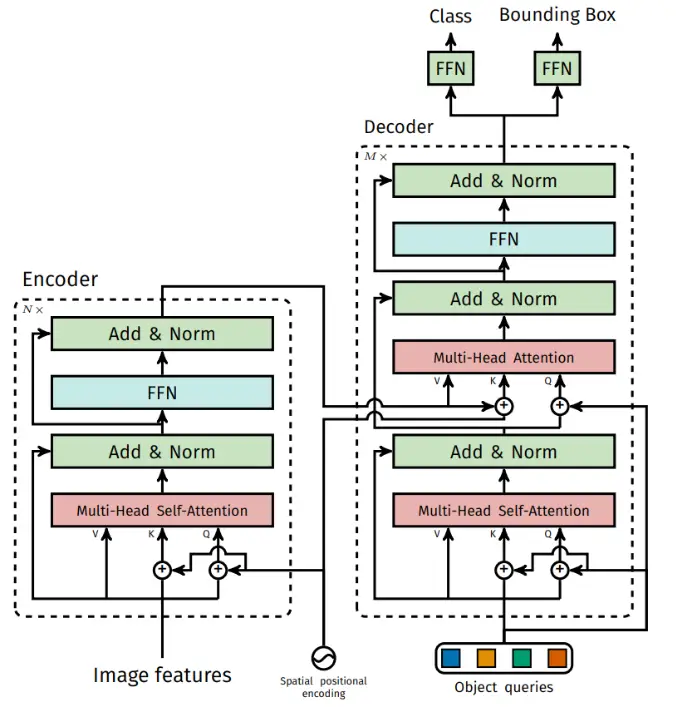
如图所示，DETR的输入是彩色图片x_{img} \in \mathbb{R}^{3 \times H_0 \times W_0}，经过CNN backbone对其进行patch处理，分成32\times32个patch。经过CNN后的特征图大小为f \in \mathbb{R}^{C \times H \times W}，其中H = \frac{H_0}{32},W = \frac{W_0}{32}，然后利用一个1*1的卷积对特征图的维度进行降维处理（相当于对C做了全连接），得到z_0 \in \mathbb{R}^{d \times H \times W}，接着把z_0进行压平处理，得到\mathbb{R}^{d \times (H \times W)}的特征图（这样相当于把图变成了和NLP中词向量序列一样的东西，词向量的维度是d，共有H*W个词向量），然后对这个特征图进行位置编码后送入Transformer Encoder中进行特征的重构，Encoder的输出特征图的维度仍然是\mathbb{R}^{d \times (H \times W)}。

接着，初始化N个object query（使用0+位置编码进行初始化），每个object query的维度是d。这N个object query首先通过Multi-Head Self-Attention层进行特征重构，输出仍为N个d维向量。接着，以Encoder的输出为K，V，重构的query为V输入Multi-Head Attention进行进一步特征重构，再经由FFN进行一次映射。整个Decoder的输出就是N个d维向量。

对这N个向量依次利用两个FFN预测头进行分类和回归就可以得到预测框的类别和Bbox。

事实上，Decoder是由M个一样的模块堆叠而成的，每个模块的输出都可以被送到预测头进行分类和回归。因此，作者对Decoder进行了深监督，即将每个Decoder层的输出通过一个共享的LN层进行归一化，然后用预测头进行分类和回归，计算loss，然后加入到总Loss中。